Pythagorean Theorem Pythagorean Theorem Pythagorean Theorem


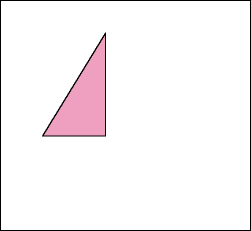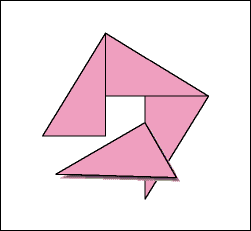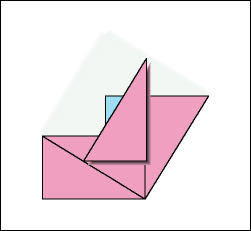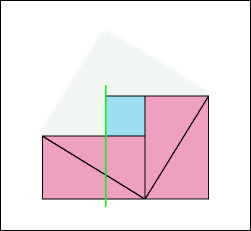Pythagorean Theorem, animated proof The famous Pythagorean Theorem, due to the Greek geometer and mathematician Pythagoras (born on the Greek island of Samos circa 580 B.C.E.), asserts that a remarkable and, at the same time, simple relationship exists between the squares of the sides of a right plane triangle. Namely, that the sum of the squares of the two sides adjacent to the right angle is always exactly equal to the square of the side opposite the right angle, the hypotenuse.

Can you see the proof of this theorem in the animation?

Some hints —   Bear in mind that the area of a square is equal to its height times its width, which, because the height and width are identical, is just the "square" of any side. Also, focus on the constancy of the total area of the figure, once all four triangles and the small blue square are in place. Finally, think carefully about what determines the widths of the two square areas separated by the vertical green line at the end of the animation (which repeats after a short pause).

If the hints aren't sufficient, don't despair!   The animation on the next page is designed to remove any, and all, mystery.



Bibliography

  1. "The Ascent of Man" by Jacob Bronowski, Little, Brown and Company, ISBN 0-316-10930-4, (1973). See in particular chapter 5, and Figure 67 on page 159, from which the animations on this web site are inspired.

  2. "The World of Mathematics" by James R. Newman, ed., Simon and Schuster, (1956). Chapter 4, vol. I, pp. 189-192, contains a proof of the theorem due to Euclid.



Copyright Notice:   The animation on this page is a copyrighted work of Davis Associates, Inc.   Permission is granted to copy and display the animation provided that the following copyright notice is displayed in a clearly legible font in close and obvious proximity to the display of the subject animation:

Copyright © 1998 by Davis Associates, Inc.
All Rights Reserved


Return to Home Page.
Davis Associates, Inc., logo Davis Associates, Inc. • 43 Holden Road • Newton, MA 02465 U.S.A. • 617-244-1450 • 617-964-4917 (Fax)
    Unsolicited advertisements not accepted at this Fax number and will be reported to the FCC.